Playing With Waves

INTRODUCTION
This lesson will build on your wave code from the last lesson, changing boundary conditions, initial conditions, and adding additional physics in the form of dissipation.

You should be starting with a code that sets an intial displacement (and presumably initial zero velocity) - a 'plucked' string. The resulting evolution should look like two identical pulses moving in opposite directions. With reflecting boundary conditions (the ends of the strings are held fixed), a pulse bounces off the end and comes back inverted. In the example shown below we have used a Gaussian funtion to define the initial displacement.

x    = linspace(-0.5,+0.5,N)
ynow = exp(-100.*x**2)

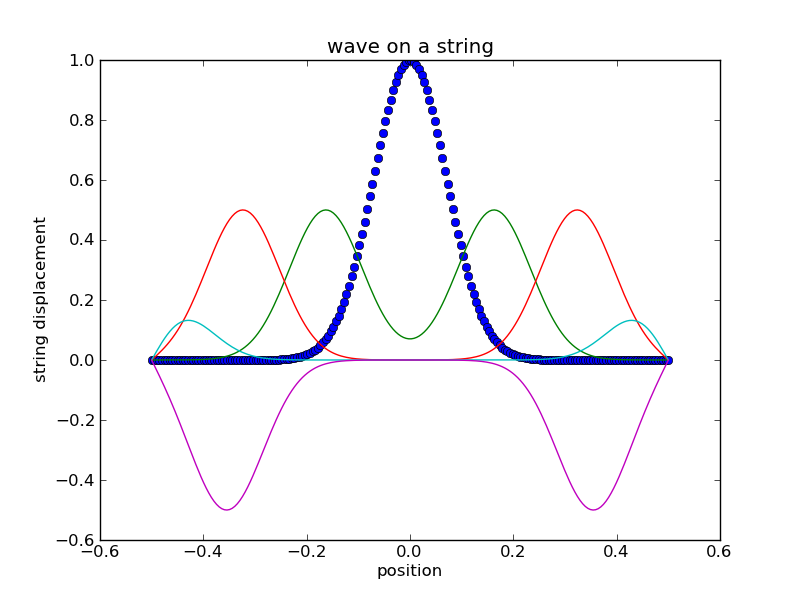
Lets begin by taking a close look at the results from our simulations in the last lesson. We can use these to verify that two solutions to the wave equation, when added together, produce another solution to the wave equation. This feature of linear superposition may appear trivial, but it is an important property of the wave equation. It implies that two waves can pass through each other without any change. For example, if you take the first case from last lesson in which an initial Gaussian displacement generated two oppositely-moving waves and let them "collide", after passing through each other they will look exactly the same as before the collision.

EXERCISE: Examine the collision of two waves, and verify that the collision does nothing to the wave forms (they look exactly the same before as after the collision).

The next task is to apply a little physics and modify the initial conditions so that there is only one wave pulse. We start by examining the generic solution to the wave equation:

Here G is a wave traveling to the left and H is a wave traveling to the right. Imagine some feature on the wave (say the crest of a water wave) is represented by the point a in the function G. As time increases, this point represented by G(a) occurs at a physical position x that must decrease with time so that the value of a = x+vt remains constant.

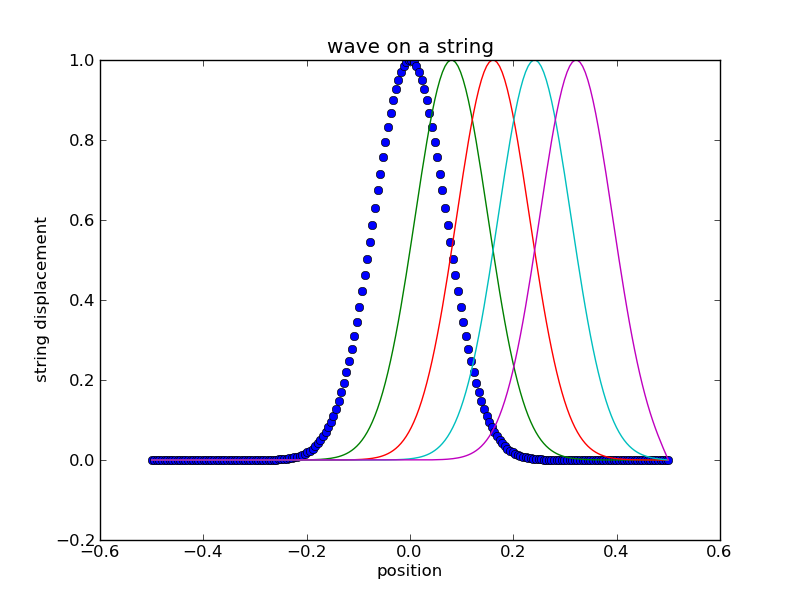
Your goal is to define initial conditions so that H is not zero and G is identically zero. You already have a definition for the initial displacement - you want this to be your entire wave function H. You need to figure out what your wave shape looks like at one time step before t=0. What is should your pulse shape look like at a time of t = -dt?

EXERCISE: Generate a Gaussian wave packet traveling to the right.

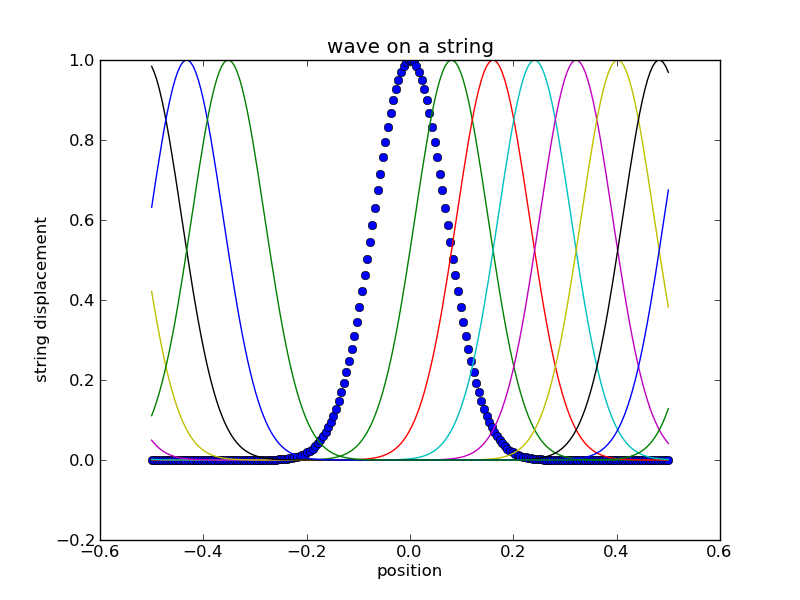
Now make your boundary conditions periodic, so that the wave moves off the right end of the string and comes back on from the left end. Instead of setting the left-most piece of string to a fixed height of zero,

ynew[0] = 0.0

you want to set it to the height of the string on the right-hand side.

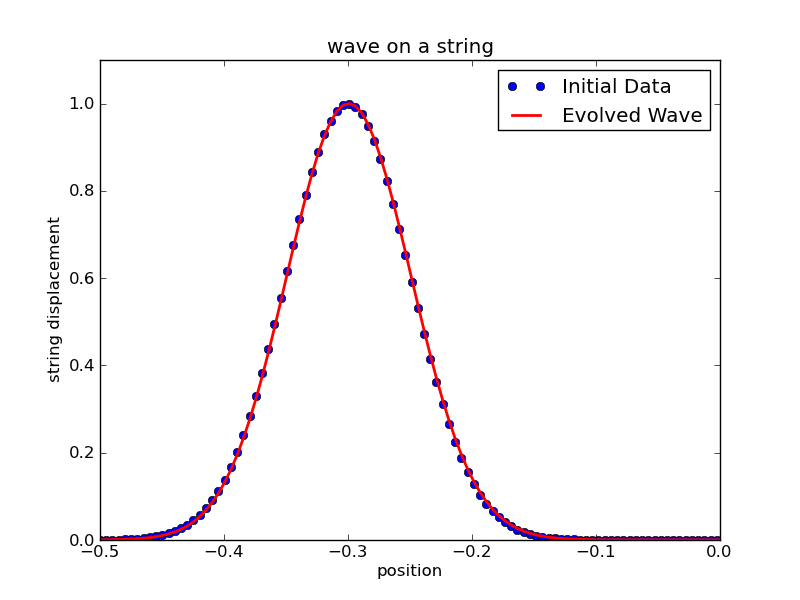
You can use this set up to quantitatively compare an evolved pulse to the original pulse to see the effects of the numerical algorithm. In the example used here, the length of the string is one (but be careful with your treatment of boundary conditions - which zones are 'active') and the speed of the wave is one, so if you plot the initial results and the state of the string at a time of one, the wave should have returned to its original position. A qualitative comparison plotted below shows that the pulse maintains its shape relatively well.

REFLECTION & TRANSMISSION
Now consider the reflection and transmission of waves at an interface separating media with differing wave speeds. Think of light going into or out of a prism. If a wave is travelling in region 1 with a wave speed of v, and it traverses an interface into region 2 where the wave speed is w, the amplitude of the reflected and transmitted waves are given by

Note that if v > w (the wave is going into a medium with a slower wave speed), the reflected amplitude is negative. What does a negative value mean for your problem of a wave on a string?

EXERCISE: Illustrate the partial transmission and reflection of a wave at an interface representing the separation of two different domains with different wave speeds. Do your wave simulations match the amplitude equations given above?

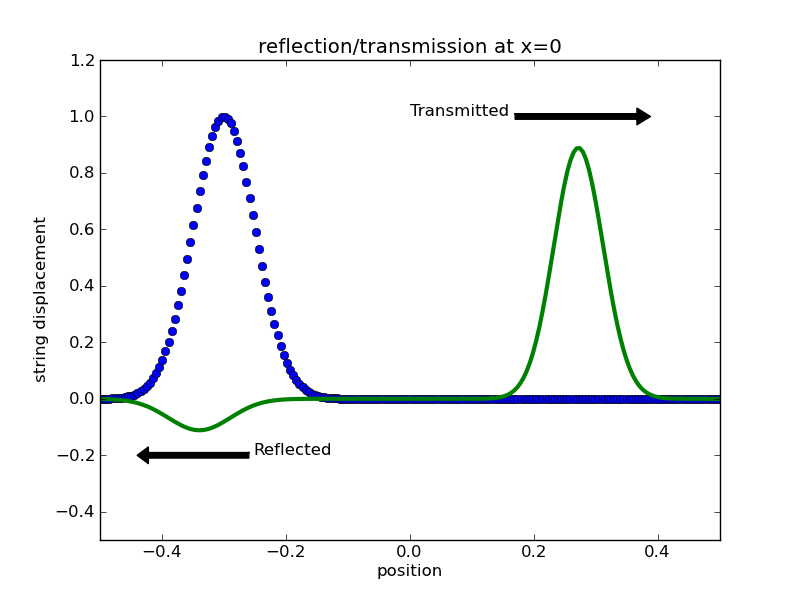
Assignment: Submit a working wave code that shows the reflection and transmission of a wave pulse that crosses a boundary where the wave speed doubles.