Lesson 26

Do The Wave

INTRODUCTION
We have seen two partial differential equations involving a scalar field, F(x,y,z); the diffusion equation

$\partial_t F(x) = D \partial_x^2 F(x)$

and Laplace's equation

$\partial_x^2 F(x) = 0$

A third common type of PDE in physics is the wave equation

$\partial_t^2 F(x) = c^2 \partial_x^2 F(x)$

These three equations represent three different mathematical types of PDEs: the diffusion equation is a parabolic PDE, the Poisson equation is an elliptic PDE, and the wave equation is a hyperbolic PDE. Although one can consider higher dimensions, the function F in each of the above equations is dependent on two variables. So in each case we are seeking a two-dimensional function for the solution. These equations require different numerical methods for solution, but they all follow the same basic idea of generating a two-dimensional solution from a given set of boundary conditions.

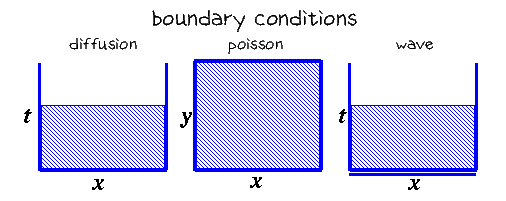
The Diffusion Equation requires three boundary conditions since there is one first-order derivative and one second-order derivative. These boundary conditions are the left (x=0) and right (x=L) boundary values for F at all times, and the initial value (t=0) for F for all space.

The Poisson Equation requires four boundary conditions, one on each bounding edge, since there are two second-order derivatives. These boundary conditions could be the value of F on the border, or the value of the tangential derivative on the border (e.g., dF/dx on the x=0 border). The first case is referred to as a Dirichlet boundary condition, the second is a Neumann boundary condition (in case you want to impress your mathematician friends).

The Wave Equation also has two second-order derivatives, but in this case the boundary conditions are the values of F on the left and right boundaries (for all time) and the value of F and dF/dt at the initial time (for all space).

The wave equation is similar to the diffusion equation in that one starts with (two) initial conditions and left and right boundary conditions, and then evolves the solution, F(x,t) forward in time. Our first approach to the wave equation will thus follow our previous solution to the diffusion equation. In later lessons we will also explore alternative solution techniques such as the spectral method.

ALGORITHM

You should be familiar with at least two different types of waves from your physics classes: acoustic waves and electromagnetic waves. In the case of acoustic waves, F would be the pressure in the air, and c would be the speed of sound. For electromagnetic waves, F would represent the time-varying electric field, and c would be the speed of light.

The simplest approach to solving the wave equation is the same tack we have taken throughout the course; replace the derivatives with a finite-difference formula:

${\partial^2 F \over \partial x^2} \rightarrow {F_{i+1} -2F_i + F_{i-1} \over \Delta x^2}$

(and the same for the time derivative) The wave equation can then be rewritten as

$F_i^{n+1} = 2(1-r^2) F_i^n - F_i^{n-1} + r^2 (F_{i+1}^n + F_{i-1}^n)$

Here the superscript represents the timestep, and the subscript represents the spatial location. Hence $F_i^{n+1}$ is the value of the wave amplitude at the new timestep at position i, $F_i^n$ is the amplitude at the current timestep, and $F_i^{n-1}$ is the value at the old timestep.

Exercise: Work out the derivation of the above equation and find out the definition of r.

PROGRAM
The algorithm for a wave code should look like:

  • declare arrays to store values of F along with the old and new values
  • choose values to define problem (dx, dt, c, etc.)
  • set initial conditions
  • loop over time to evolve wave
    • new F = ...
    • apply boundary conditions at the two ends
    • old F = current F
    • current F = new F
  • plot the wave

If dt is chosen too large, the numerical scheme produces garbage. A proper stability analysis tells us that the maximum value of dt is limited by dx/c.

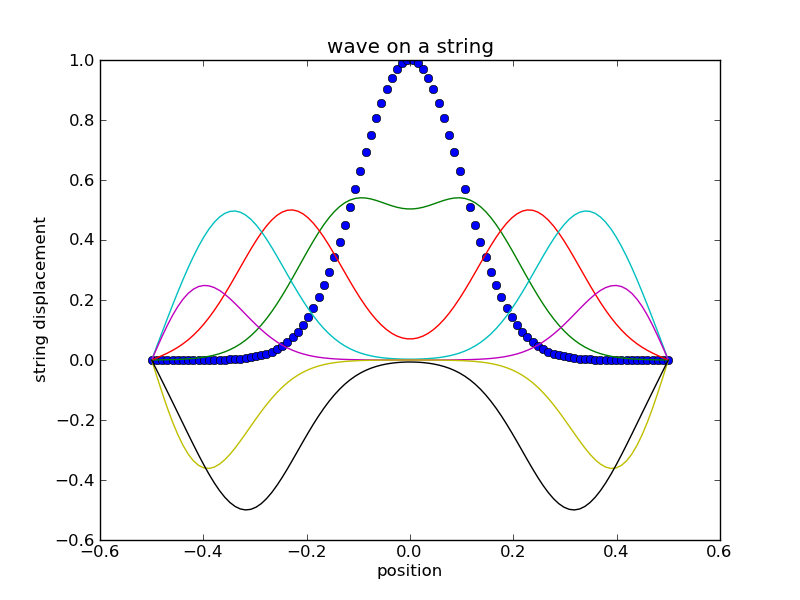
Assignment: Evolve a wave on a string.