INTRODUCTION
Another common problem in physics that can be addressed with random numbers is the
random walk. The diffusion of a photon out of the Sun, the bouncing of an ion across a shock front, or the motion of a Nitrogen molecule through this room can all be described by a random walk. The common element of these problems is the motion of particles dominated by a large number of collisions that alter the path of the particle. Lets consider the problem of physic students leaving a brutal final exam in quantum mechanics. Every student is so disoriented that he/she stops every five feet and takes off in another random direction. After 10 minutes walking at 1 f/s the students heads begins to clear. How far away from Riddick Hall are these poor souls? How spread out are they?
Our first step is to modify the problem to make it simpler the first time around, after which we can go back and implement the full problem. In this case we will make the simplifying assumption that the student only walks in a straight line, but can move in either direction along that line: the one-dimensional random walk. We can model this process making use of the random number generator to decide which direction the student walks after every 5 feet. The algorithm should look something like this...
- Start off at position x=0 at time t=0
- Random walk in 5 foot segments (at 1 f/s, each segment is 5 seconds)
- Use random() to decide the direction of the next step (forward if > 0.5, else backward)
- Increment x either forward or backward
- Record current position and time
Exercise: Write a code to compute a one-dimensional random walk as described above. Print out the final position after 50 steps. Run the code multiple times. (Don't bother with plotting the steps for now.)
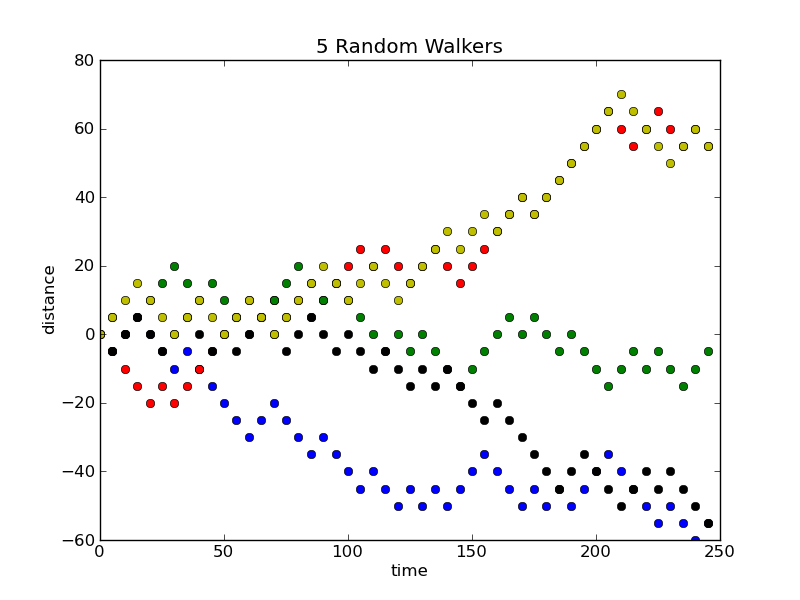
If all 40 quantum students left the front of Riddick hall in a daze, the average distance from Riddick hall after 10 minutes would be zero, since each segment is as likely to be forward as backward. This does not mean that each and every student will still be in front of Riddick Hall after 10 minutes; it means the average position of all the students combined will be in front of Riddick Hall. The students themselves will be some average distance away, but some in the forward direction, some in the backward direction. This difference is due to the fact that while the average of x is zero, the average of x2 is not!
The average distance traveled by each student is instead given by
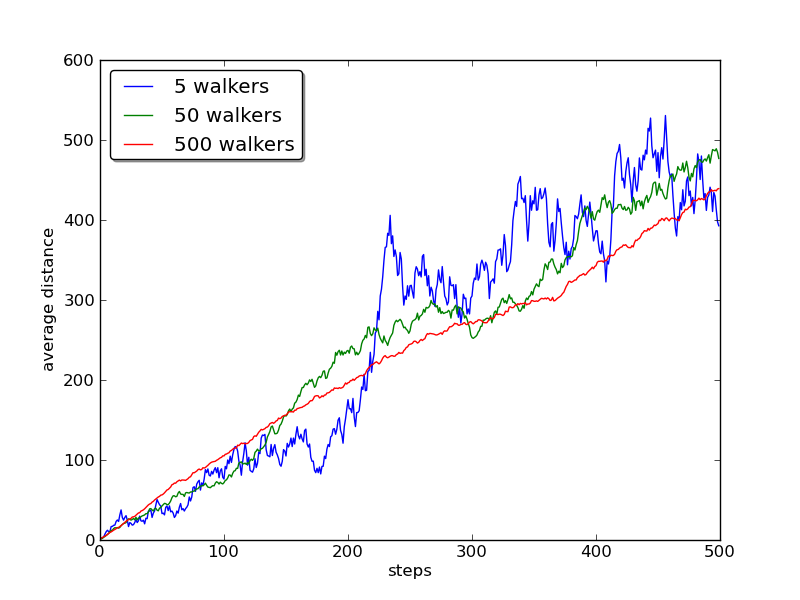
It turns out that $\langle x^2 \rangle$ increases linearly with the number of steps. Hence the average distance travelled increases with the square root of the number of steps and hence the with the square root of time.
Exercise: Verify this time dependence by plotting $x^2$ as a function of time, averaging over 500 different walkers.
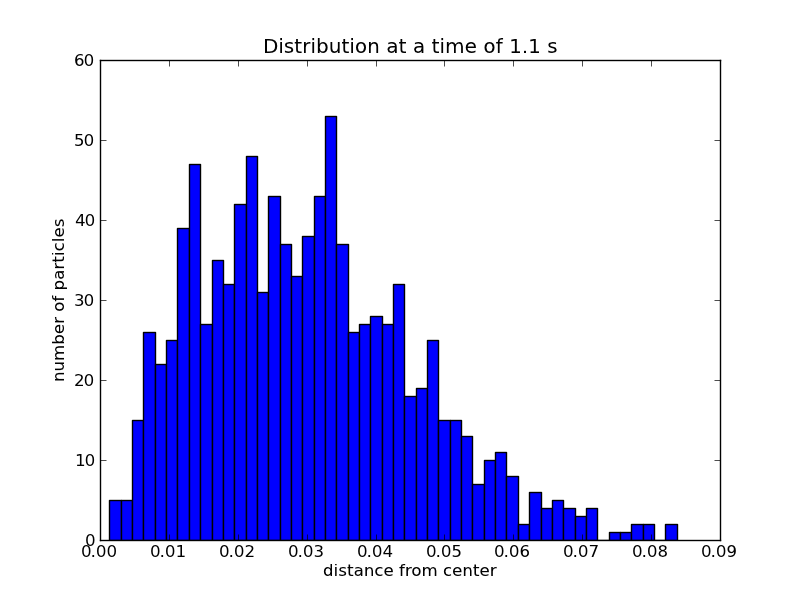
Assignment: Write a routine that simulates the Brownian motion of a set of 1000 particles on the surface of a glass of water. The partlcles are tossed around by collisions with water molecules. Assume that they all move freely for a mean free path of $\lambda = 1$ mm between collisions and their velocity is always 1 m/s. Compute the time needed for the particles to form a spot with a radius of $\sqrt{\langle r^2 \rangle} = 3$ cm where $r$ is the distance from the center of the glass, where the particles were initially deposited. Show also the radial distribution of particles $dn/dr$ with a histogram.