INTRODUCTION
Our next step on the road to chaos is to add damping and a forced driving term to our pendulum. Before jumping into that, lets take a look at some other numerical methods for solving ordinary differential equations. We saw in the last lesson that the error in the Euler method produced unacceptable results for the pendulum problem. In contrast, the Euler-Cromer method has error terms of comparable magnitude, but it has the advantageous feature of conserving energy over a single period of oscillation. One can do better than both of these methods with only a slight increase in work, but before we look at these more accurate methods, lets go back and take a look at the Euler method from a graphical viewpoint.

Our generic problem is to find a solution to an ordinary differential equation,

The Euler method amounts to using the slope at time t to make a guess for $y(t+\Delta t)$

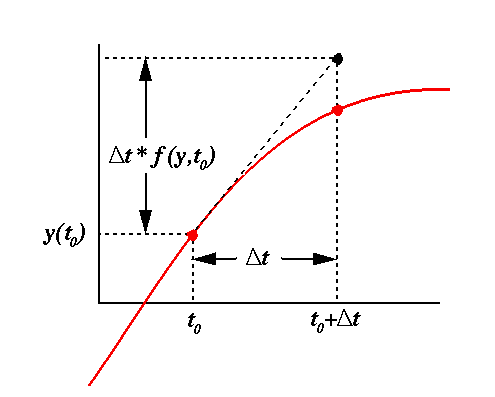
If there is much curvature in the function y(t), this guess can be far from the correct value. A more accurate guess could be obtained if one used the slope of y(t) at some midpoint between t and $t+\Delta t$. The only difference between this and the Euler method is evaluating f(y,t) at the midpoint. The value of t at the midpoint is just $t+\Delta t/2$, while the value of y at the midpoint can be found using the Euler method.

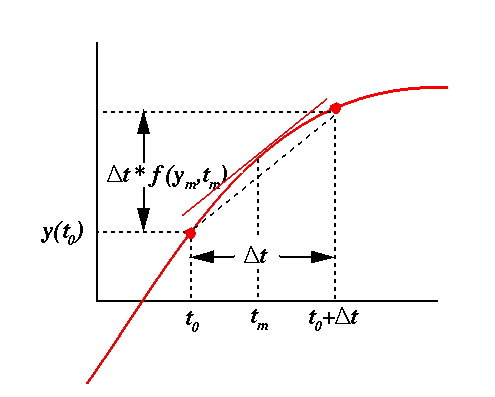
This technique is known as the second-order Runge-Kutta method. First find values at a half step forward (in time):

Then use these mid-step values to take a full step forward:

Exercise: Modify your pendulum code to use the Runge-Kutta method. Does it conserve total energy?

#Euler Method
for n in range(N-1):
  theta[n+1] = theta[n] + dt * omega[n]
  omega[n+1] = omega[n] + dt * (-g/L*sin(theta[n]))

#Runge-Kutta Method
for n in range(N-1):
  # half-step uses only values from step [n] on the right-hand side
  theta_mid = theta[n] + 0.5*dt * omega[n]
  omega_mid = omega[n] + 0.5*dt * (-g/L*sin(theta[n]))

  # full-step uses midpoint values on the right-hand side
  theta[n+1] = theta[n] + dt * omega_mid
  omega[n+1] = omega[n] + dt * (-g/L*sin(theta_mid))

Now that we have a working code to simulate the swinging motion of a simple pendulum, we can extend our model to the more interesting problem of a driven pendulum. We will add two terms to our mathematical model, one to account for frictional damping, the other to model an external driving force.

The frictional damping is proportional to the angular velocity; the faster the pendulum swings, the larger the frictional force trying to slow it down (hence it is a negative term). We will parameterize the damping using a variable, q, with a value of order unity.

The driving force will have some inherent frequency associated with it, such that this force is trying to drive the pendulum to swing at the driving frequency. The resulting mathematical model of our damped, driven pendulum is

Exercise: Add these two terms to your pendulum program, and compute $\theta(t)$ for values of the driving force of 0.0, 0.5, and 1.2. Use a damping coefficient, q=0.5, a driving frequency $\Omega_D = 2/3$, and $g = L = 9.8$.

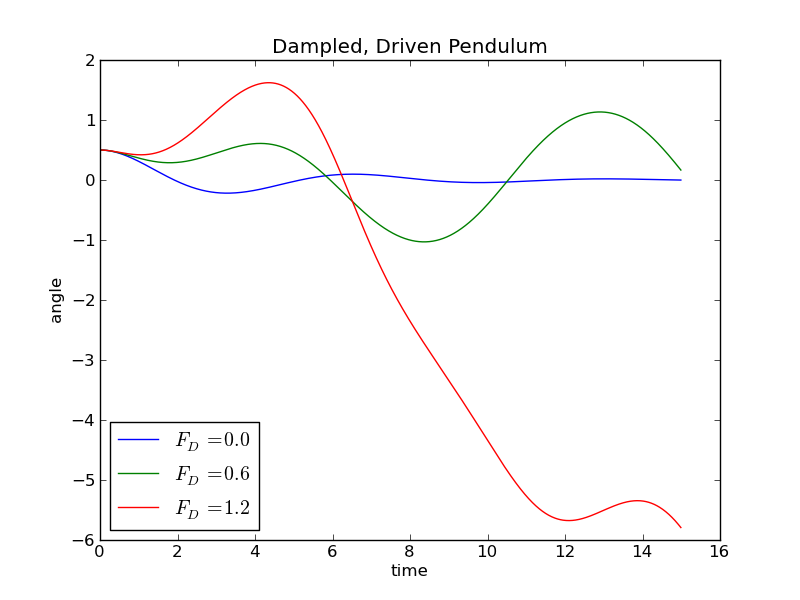
We find three rather different behaviors depending on the value of the driving force. With no driving, but with damping, the pendulum tries to oscillate at its natural frequency, but the amplitude quickly decays away due to the frictional damping. With a moderate driving force, the pendulum settles into harmonic motion at the driving frequency, not the natural frequency of the pendulum. The suprising result occurs for large values of the driving force. Here the pendulum does not dutifully follow the driving frequency, and in fact shows no sign of a periodic behavior. The value of theta exceeds pi in both positive and negative directions, indicating that our simple pendulum has swung all the way around on its pivot. It is this regime that we describe as chaotic, but what does it really mean to be a chaotic system?

Chaos
One characteristic of a chaotic system is that it is unpredictable, but are we not "predicting" the motion of the pendulum with our computer code? In this case, unpredictable relates to an extreme sensitivity to initial conditions. If we run our program with identical initial conditions, except that on run has an initial theta that is different by 0.001, we find that the pendulums move identically for a given period of time. Eventually, however, their motions diverge.

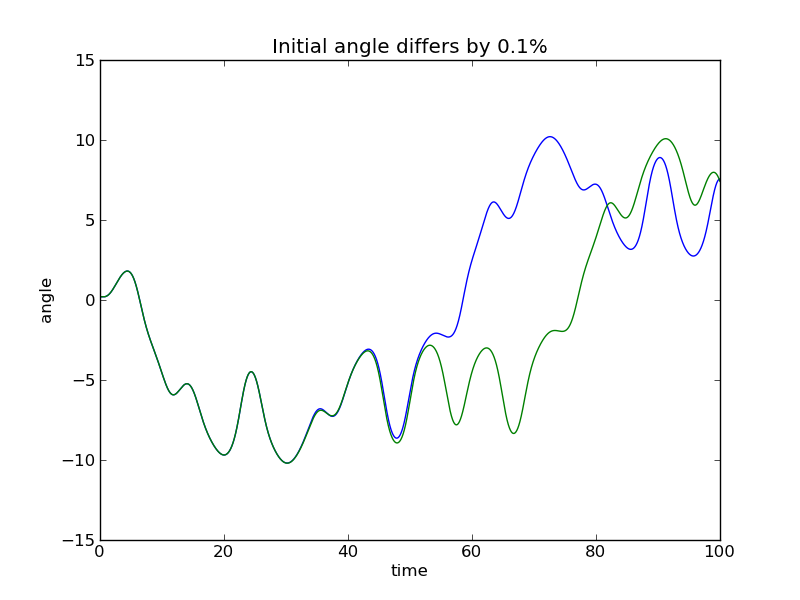
The term unpredictable thus refers to the fact that one would need to know the initial conditions to arbitrarily high accuracy if one wanted to predict the exact motion of a chaotic system for any extended time.

Assignment: Investigate the diverging motions of two nearly identical pendulums as a function of the difference in their initial conditions. Do the paths always diverge, no matter how small their initial conditions? Submit a Python program that generates a plot similar to the one shown above, showing two nearly identical pendulums.

Higher Order Runge-Kutta Methods
One can extend these 'mid-point' corrections to higher order. In fact, the term Runge-Kutta method generally refers to the fourth-order version. Before describing this RK4 method, lets go back and write down the second-order method in slightly simpler terms. Here we consider a function f(y,t) and a step size of h in the independent variable, t.

The RK4 method can then be written as