INTRODUCTION
There are occasions when you are simply given a set of data for some quantity as a function of another. This might be the data from some experiment or it might be some data from a complicated calculation. Examples are: the x-velocity vx of a vehicle at various times t, the electric potential V due to a complicated distribution of charge at points x, the pressure P of a gas at various temperature T, and you can think of many many more. Typically, however, this data is going to have some scatter to it. As a concrete example, say we performed an experiment in which we drop a ball and record its velocity as function of time. From this data we want to find the acceleration due to gravity. Here is an example dataset: freefall.data. The first column is a list of times at which the measurements were made, the second column is the velocities at those times.

The first task is to read this data into Python and plot it as a bunch of points. In this simple case of columns of numbers the procedure is simple:

from matplotlib.pylab import *
freefall=loadtxt('freefall.data')

This command reads in every line of data in the file freefall.data and loads the columns of numbers into the 2D array freefall. The first column of numbers (the times) are stored in freefall[:,0], and the second column (the velocities) in freefall[:,1]. The length of the second dimension of the array freefall corresponds to the number of columns in the data file being read; if there were more columns, the second dimension of this array would larger. You can now plot this data as points. Here we copy each column into its own array to make the reference within the code easier to read.

time  = freefall[:,0]
speed = freefall[:,1]

plot(time,speed,'ro')
axis([0,1.0,0,10.])
xlabel('time (s)')
ylabel('speed (m/s)')
show()

The result should be something like this...

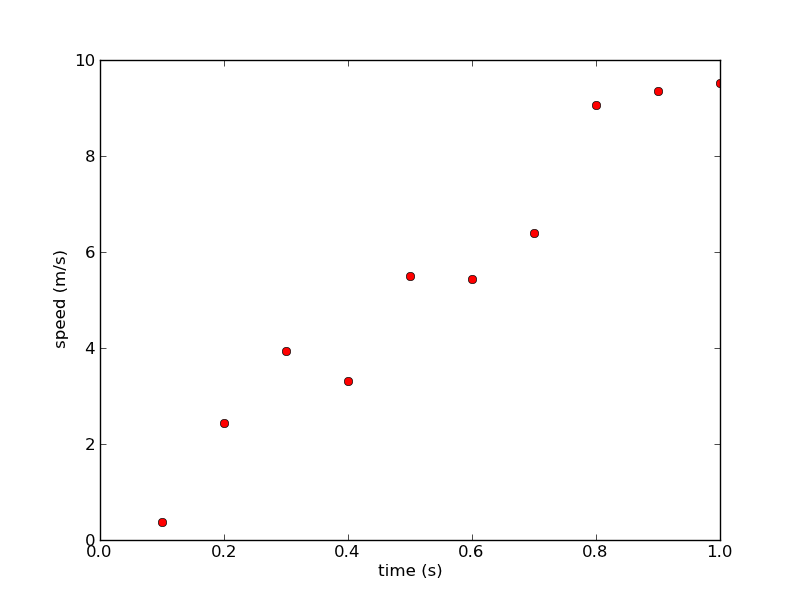
Of course you know what the data should look like if you had infinite precision in taking your data. Use the plot command to add a line showing the expected behavior. Suppose, however, that you did not know the expected behavior, or you are trying to use this data to test a hypothesis. In this situation you are faced with trying to find the 'best fit' mathematical function to represent the data.

Least Squares Fit
Let us assume you have some data from an experiment. Your data has the generic form of pairs $x_i,y_i$. Now we are looking for an approximating function $f(x)$ which describes the data. We do not require the function to go through any specific data point. Rather, we are looking to describe the data as whole. For our definition of “best fit” we will use a very simple definition: we require that a certain estimate of the error is a minimum. The error between the data and our approximating function describes the difference between our guess (the approximating function) and the data. Or in other words, the error measures the difference between calculated value and measured values. This difference can be positive or negative. Hence, we will use the square of the difference to obtain all positive numbers. Now we can add all the differences:

We will obtain our approximating function by making this error as small as possible through adjusting the parameters in the function $f(x)$.

The first step is making a guess at the form of the function describing the data. What function $f(x)$ are you trying to fit? For our freefall example our guess is:

Now we need to minimize the error

by varying the parameters a and b. The error S will be minimal whenever $\partial S / \partial a = 0$ and $\partial^2 S / \partial a^2 > 0$ and whenever $\partial S / \partial b = 0$ and $\partial^2 S / \partial b^2 > 0$. Evaluating these derivatives, we find for this example the following two equations which determine the values of a and b:

All we need to do is find a and b such that these equations hold (everything else in these equations is a known quantity). You could solve this equation by hand, but you should recognize it as a linear algebra equation. If we define the matrix

and the vector of constants

then this equation can be written in the familiar form Ax=c, where x is our vector of unknowns, a,b. The solution can easily be found with the numpy.solve function:

from matplotlib.pylab import *
A = [[a11,a12],[a21,a22]]
c = [c1,c2]
x = solve(A,c)
a = x[0]
b = x[1]

Assignment: Write a program to determine a and b in the above example using the linear algebra solve package to find the values of a and b that minimize the 'error.' Plot the velocity data and your best fit to that data.

leastsq
While it is not a lot to code up this simple example, you can imagine this process quickly getting out of control. In practice, you can usually find a Python function written by someone else (with a little more experience). In this case, we could use the optimize.leastsq function provided in SciPy. An introduction to this function is provided in the SciPy Cookbook.

The leastsq function requires a definition of the error (difference between the value given by the fitted funtion and the data), an array of parameters from the fitting function that will be solved for, and the data being fitted. We already have our data in the arrays time and speed.

The next step is to define a function we want to fit to our data, in this case a straight line with y intercept a and slope b, which we reference in our program below as x[0] and x[1]. Given two scalar values for x and an array of times, time, fitfunc(x,time) returns an array of computed values of the speed at each value of time according to our linear function.

We then use this fitting function to define our error, which in this case is simply the difference between our fitted value and our data value. At each value in the array time we compute a fitted value and subtract off our data value. The returned result is an array (of the same length as our data vectors) of fitting errors.

The last step is to make a guess for the coefficients x0[0] and x0[1]. Calling the leastsq routine then adjusts these coefficients to minimize the error, returning the 'best fit' values of the coefficients in the new vector x1. Putting it all together we have:

from matplotlib.pylab import *
from scipy import optimize

# Read in the data, storing it as two 1D arrays, time and speed
freefall=loadtxt('freefall.data')
time  = freefall[:,0]
speed = freefall[:,1]

# Define the function you want to fit to the data
def fitfunc(x,t):
  z = x[0] + x[1]*t         
  return z

# Define the error as the fit function minus the read data
def errfunc(x,t,v):
  z = fitfunc(x,t) - v  
  return z  

# Provide an initial guess for constants a and b
x0 = [1.0,8.0]                                


# Call the scipy routine, passing it your definition of the error function, initial guess, and data
x1, success = optimize.leastsq(errfunc, x0, args=(time,speed))

# Print out the key result, the measured value of gravitational acceleration
print 'g = ', x1[1], ' m/s'

# Create an array of times from the minimum value in the array time to the maximum value
t1 = linspace(time.min(),time.max(),100)

# Plot the original data, along with the fitted function
plot(time,speed,"ro",t1,fitfunc(x1,t1))
show()