Numerical Integration I

INTRODUCTION Throughout all areas of physics we often meet the integral: work is the integral of a force along a path, Gauss’ law is that surface integral of the E⃗ field is equal to the enclosed charge, the action is the integral of the Lagrangian, and many many more. But before we can tackle line integrals, surface integrals and all the rest we shall start with the simplest problem of the definite integral of a function with a single variable.

EXAMPLE: Electric Potential Let’s have a specific application in mind: the electrostatic potential of a finite segment of charged wire of length 2L, at a height H above the center of the wire.

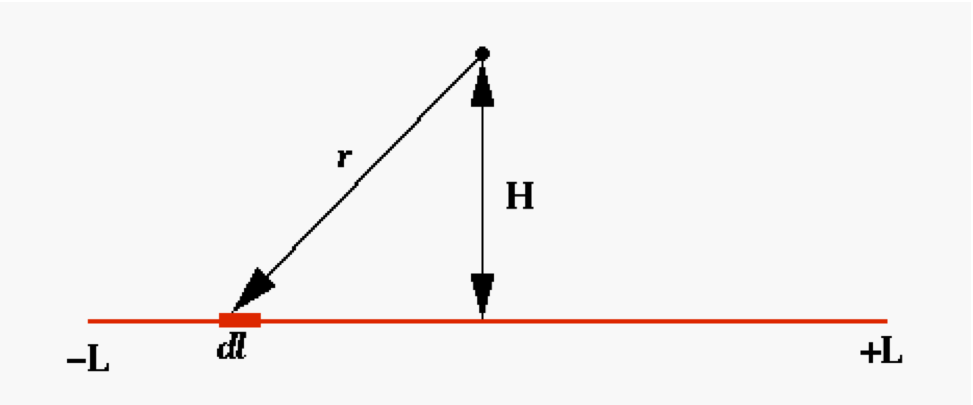
If the charge per unit length is $\lambda$ then the potential V is

where $r^2 = l^2 + H^2$. If $\lambda$ is a constant, this problem is sufficiently easy that you can compute it analytically. (Do it!) For the choice $L=H$ the answer is $V = 1.7627 \lambda/(4\pi\epsilon_0)$. But what if the problem was harder? For example, how would you solve it if the charge density varied along the wire as

Riemann Integration If you ask your math major friends they will tell you there are a dozen different definitions of an `integral' (I bet you never knew that) but the working definition we shall use is the Riemann integral. This definition of the integral doesn't always work in practice - some integrands cause problems - but it's good for 99% of situations like the one here. Say we have a function f(x) and we wish to know its integral between two points x=a and x=b i.e.

Let's insert $N-1$ points between $a$ and $b$, where $N$ is some integer, and we'll call them $x_1$, $x_2$ up to $x_{N-1}$. The new points don't have to be equally spaced between $a$ and $b$ but often times they will be. Let's also assign $x_0$ as an alternative name to point $a$ and $x_N$ as an alternative name for $b$. With the new points we have divided up the integration domain into $N$ subintervals - this is called `partitioning' the interval - and the `mesh' of the partition is the largest subinterval i.e. the largest separation between adjacent $x$'s. Then, between each pair of $x$'s we insert points $t_0$ to $t_{N-1}$: they don't have to be halfway between the $x$'s, they can be on one side or the other of the subinterval or even randomly placed. Once we've done all that, we compute something known as the Riemann sum

The Riemann definition of the integral is that the integral $\int_a^b f(x)\,dx$ is equal to the value of the Riemann sum I in the limit where the mesh tends to zero. This definition is the mathematical statement that the integral is the `area under the curve' and sometimes one sees this `area under the curve' idea used instead of the limit of the Riemann sum. Either way, in practice one has three choices to make before using this formula:

1. Where do we put the $x$'s?
2. Where do we put the $t$'s?
3. How do we take the limit?

The different choices we can make lead to a whole zoo of different numerical integration methods.

Rectangle Methods The simplest way to select the x's is to pick a value of N and then put them uniformly between $a$ and $b$. That way the mesh, $h$, is $h=(b-a)/N$ and the subintervals are all the same size $h$. The Riemann sum is then

What shall we do for the $t$'s? The three most obvious places to put them is either the left hand side, the middle, or the right hand side of the subintervals. Let's leave the choice of the middle point for the time being and concentrate on the other two: putting the $t$'s on the left or right hand side of the subintervals. If we use the idea that the integral is the area under the curve then we see that what we are computing for both choices of the $t$'s is the area of a rectangle whose width is $h$ and whose height is $f(t_n)$. Your job now is to make this algorithm reality.

We are going to integrate the function $\sin(x)$ between $x=0$ and $x=\pi/2$.

EXERCISE: What is the exact analytic result?

We are eventually going to write a code using the left and right rectangular methods but first we shall do by hand what we shall later ask the computer to do.

1. The left and right rectangular methods divide the interval $a$ to $b$ into $N$ subintervals. Using $N=4$, what are the widths $h$ of the rectangles.
2. Using the widths of the rectangles computed in step 1, what are the boundaries of the first subinterval i.e. $x_0$ and $x_1$
3. The left rectangular method puts the $t$'s on the left hand side of the subintervals, the right rectangular method puts them on the right hand side. For the first subinterval, what is the value of $t_0$ for the left rectangular method and the value of $t_0$ for the right rectangular method?
4. Evaluate the function at $t_0$ for the two methods.
5. Compute the boundaries for the second subinterval.
6. Compute the values of $t_1$ for the two methods.
7. Evaluate the function at these value of $t_1$ and add it to the value you got from step 4.
8. Repeat steps 5-7 but now for the third subinterval.
9. Repeat steps 5-7 but now for the fourth subinterval.
10. Multiply your sum of the function evaluations by the width of the rectangles $h$ from step 1. This is your result for the Riemann sum

Now we are going to write in code form the list of steps from the previous exercise and we shall do it for both the left-rectangular method and for the right-rectangular method.

EXERCISE: Write a python code to compute the integral/Riemann sum using the left and right rectangular methods for the function $f(x)=\sin(x)$ between $x=0$ and $x=\pi/2$ for a given value of $N$. Before you start, think carefully about how to structure your code. Some questions you will need to consider: what variables and functions will you need to define? How will you step through the subintervals? How will you keep track of the sum of function values?

Assignment: Make a plot of the error as a function of $1/N$. Roughly how does the error scale with $1/N$? What do you notice about the errors between the two methods?

A Warning As stated above, there are more integration methods out there than you ever want to meet. Basically they all boil down to approximating the function $f(x)$ with some other function, either over the whole interval or over some some small part of it, whose integral can be done by hand. Then, this method may be combined with other methods to eliminate the highest order numerical error or extrapolated to the limit where $N \rightarrow \infty$. But no matter how sophisticated these routines become they will all break down if any of the function evaluations cannot be done. Consider the following integral:

If you use the rectangular methods from above and it tries to evaluate the integrand at $x=0$ you will meet your grandmother even though the integral does exist: the answer is 6. This kind of integral is known as an 'improper' integral and these kinds of integrals often causes numerical routines problems. There are other integrals out there which look very similar to improper integrals, e.g.

But this is an `impossible' integral and it has no answer no matter what method you use. This all goes to show you yet again that you will run into trouble if you just blindly apply an algorithm without examining whether the algorithm is suitable to the problem at hand. Be warned.