Lesson 10

Linear Algebra II

INTRODUCTION The previous lesson introduced the problem of solving for a vector of unknowns, v, in the equation Av=r, where A is a matrix and r is a vector of constants. Another very important class of problems in linear algebra has the form $M v = \lambda v$. Here, $M$ is a matrix, $\lambda$ is a single number, and $v$ is a vector. This is the eigenvalue/eigenvector problem.

EXAMPLE: Coupled Oscillator Again we go back to basic mechanics for an example. Consider two masses moving in one dimension along a friction--free table. The masses, both of mass m, are connected by identical springs to a fixed wall, as shown in the figure below. Each spring has stiffness $k$ and relaxed length $\ell$. Let $x_1$ and $x_2$ denote the positions of the masses as measured from the wall.

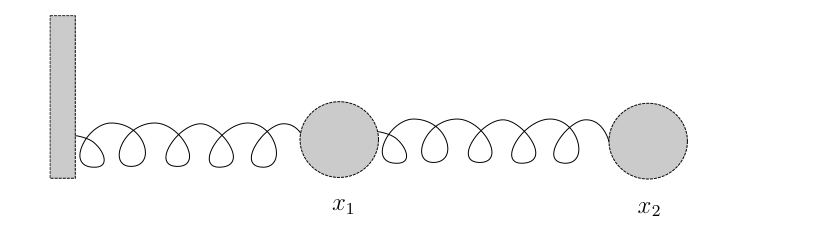
If you displace one or both of these masses from its equilibrium point and let it go, you would see a complicated motion of both masses. This complex evolution can be more easily understood in terms of the two normal modes of the system. To better understand these normal modes (which we will get from the eigenvector analysis), let us first review the simpler problem of only one mass on one spring. In this case we are solving the simple equation

$m \ddot x_1 = -k x_1 $.

Recognizing that the solution to this is a harmonic function, we can write down the generic solution as:

$x_1 = A\sin(\omega t) + B\cos(\omega t)$

where $\omega = \sqrt{k/m}$ is the frequency of oscillation of the mass. The constants A, B are determined by the initial conditions of the system (initial displacement and velocity). The motion is thus very simple, oscillating back and forth with this fixed frequency.

Extending this to our two-mass system starts off the same way, applying Newton's second law to each mass:

$m \ddot x_1 = -k(x_1 - \ell) + k(x_2 - x_1 - \ell) \\ m \ddot x_2 = -k(x_2 - x_1 - \ell)$

The normal mode analysis is a powerful technique used to characterize an oscillating system. A normal mode is a pattern of oscillation in which each part of the system vibrates about its equilibrium position at a common angular frequency $\omega$. Thus, for this system the normal modes have the form

$x_1 = \ell + A\sin(\omega t) + B\cos(\omega t) \\ x_2 = 2\ell + C\sin(\omega t) + D\cos(\omega t) $

Inserting these expressions into the differential equations, we find

$ -m\omega^2 [A\sin(\omega t) + B\cos(\omega t)] = \\ k[C\sin(\omega t) + D\cos(\omega t) - A\sin(\omega t) - B\cos(\omega t)] - k[A\sin(\omega t) + B\cos(\omega t)] \\ -m\omega^2 [C\sin(\omega t) + D\cos(\omega t)] = \\ -k [C\sin(\omega t) + D\cos(\omega t) - A\sin(\omega t) - B\cos(\omega t)] $

By setting $t = 0$, we find that the coefficients of $\cos(\omega t)$ must vanish. Likewise, by setting $t = \pi/(2\omega)$, we find that the coefficients of $\sin(\omega t)$ must vanish. This leads to the following four equations:

$m\omega^2 A = kA - k(C-A) \\ m\omega^2 B = kB - k(D-B) \\ m\omega^2 C = k(C-A) \\ m\omega^2 D = k(D-B) $

which can be written in matrix notation as

$\left(\begin{array}{cccc} 2 & 0 & -1 & 0 \\ 0 & 2 & 0 & -1 \\ -1 & 0 & 1 & 0 \\ 0 & -1 & 0 & 1 \end{array}\right) \left(\begin{array}{c} A \\ B \\ C \\ D \end{array}\right) = \omega^2 m/k \left(\begin{array}{c} A \\ B \\ C \\ D \end{array}\right)$

This is an eigenvalue/eigenvector problem, where the eigenvalue is $\lambda = \omega^2 m/k$ and the eigenvector is the set of amplitudes $v = (A,B,C,D)^T$. Note that an eigenvalue of $\lambda = 1$ corresponds to the natural frequency of one mass on one spring, $\omega^2 = k/m$.

Eigenvalues and Eigenvectors We have now reduced our two-masses on two-springs problem into the mathematical form of $M v = \lambda v$. The right--hand side of this eigenvalue/eigenvector equation can be written as $\lambda I v$ where $I$ is the identity matrix. With this notation the problem can be written as $A v = 0$ where the matrix $A$ is defined by $A \equiv M - \lambda I = 0$. Of course, we know how so solve the system $Av =0$: simply invert the matrix $A$ and mutiply both sides of the equation by $A^{-1}$. This yields the trivial solution $v = 0$. Note that $v=0$ is always a solution to our original problem, $Mv = \lambda v$. In fact, it is the only solution assuming that the matrix $A \equiv M - \lambda I$ is invertible. For certain special values of $\lambda$, called eigenvalues, this matrix will {\em not} be invertible and the system $M v = \lambda v$ will have nontrivial solutions for $v$. The nontrivial vectors $v$ are called eigenvectors.

The eigenvalue/eigenvector problem consists of finding all of the eigenvalues $\lambda$ such that $M - \lambda I$ is not invertible, then (for each eigenvalue) finding the corresponding eigenvectors $v$ that satisfy $Mv = \lambda v$. In python, you can use the numpy function eig() to solve the eigenvalue/eigenvector problem. More precisely, the command

eigenval,eigenvec = eig(M)

will compute the eigenvalues and corresponding eigenvectors of a matrix $M$. The eigenvalues are placed in an array, called eigenval in this example. The first eigenvalue is stored in eigenval[0]: 

>> print eigenval[0]
-2.0

The eigenvectors are placed in a matrix, called eigenvec in this example. The first column of eigenvec is the eigenvector corresponding to the first eigenvalue. The second column of evec is the eigenvector corresponding to the second eigenvalue, etc. 

>> print 'The first eigenvector is ', eigenvec[:,0]
The first eigenvector is [-0.70710678  0.70710678]

EXERCISE: Consider the matrix

$M = \left(\begin{array}{cc} 1 & 3 \\ 4 & 2 \end{array}\right) $

Issue the command eigenval,eigenvec = eig(M). This should yield the eigenvalues $\lambda_1=-2$ and $\lambda_2=5$, with the corresponding eigenvectors $v_1 = (-0.707, 0.707)^T$ and $v_2 = (-0.6, -0.8)^T$. Verify by hand calculation that these eigenvalues/eigenvectors satisfy $Mv = \lambda v$. Note that the eigenvector associated with a given eigenvalue is not unique: If $v$ satisfies the equation $Mv =\lambda v$, then so does any vector proportional to $v$. Thus, for this problem, we can rescale the eigenvector associated with $\lambda_1$ to obtain $v_1 = (1,-1)^T$. Likewise, we can rescale the second eigenvector to $v_2 = (3,4)^T$. Verify by hand that these new eigenvectors satisfy $Mv = \lambda v$.

Now apply this process to the coupled masses on springs. The first task is to find the eigenvalues, which represent the frequencies of the normal modes of the system, and the eigenvectors, which describe the relative amplitudes of the harmonic functions making up each corresponding normal mode. The second task is to use these results to describe the motion of the normal modes.

Assignment: Use Python to solve the eigenvalue/eigenvector problem numerically and then plot the motions of the two normal modes. Let $k = 15$ and $m = 0.3$ in SI units. For each eigenvalue $\lambda$, identify the corresponding eigenvector and compute the frequency $\omega = \sqrt{\lambda/m}$. For each eigenvalue, plot a graph showing $x_1 - \ell$ and $x_2 - 2\ell$ as functions of time. These are the normal modes of vibration for the system. Describe qualitatively the difference between the normal modes. The most general motion of the system is a linear combination of normal modes.