INTRODUCTION Linear algebra is one of the most important branches of mathematics, with applications found in almost every branch of physics. The techniques of linear algebra also form the basis of many numerical algorithms used in mathematics, science and engineering. In this lesson, you will learn to translate linear algebraic systems into matrix–vector notation and to solve these problems using built–in python commands. These techniques will be applied to problems in statics, electric circuits, and periodic motion.

EXAMPLE: Static Equilibrium Consider the all-too-familiar problem of a static beam connected to a wall and suspended with a cord under tension, as shown in the diagram below. The cord makes an angle $\theta$ with the beam, and has tension $T$. The wall exerts a force on the beam with components $F_x, F_y$.

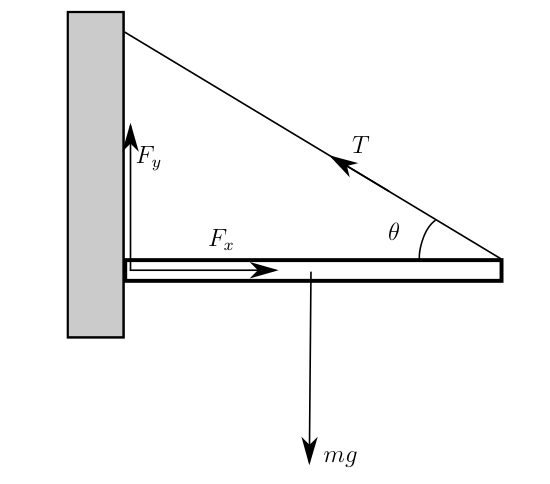
The beam is in static equilibrium, so the sum of forces must vanish, $\sum \vec F = 0$, and the sum of torques about any point ${\cal P}$ must vanish, $\sum \vec \tau_{\cal P} = 0$. All forces lie in a common plane, namely, the $x$--$y$ plane. Thus, $\sum \vec F = 0$ reduces to two equations, one for the $x$--component and one for the $y$--component. Likewise, $\sum\vec \tau_{\cal P} = 0$ reduces to a single equation for the $z$--component. If we use the middle of the beam as the point ${\cal P}$, the three equations are

Assuming $m$, $\ell$ and $\theta$ are known, these three equations can be solved for the three unknowns, $F_x$, $F_y$ and $T$. This is a simple example of a system of three coupled linear algebraic equations.

To illustrate the basic idea, lets consider an even simpler set of two coupled linear equations:

How do you find $x$ and $y$? Using the straightforward approach, you can solve one equation for one variable, substitute the solution into the other equation, then solve for the remaining variable. For example, solving the first equation for $x$ we obtain

Substituting this result into the second equation yields

with the solution $y = −2$. Using this value in the first equation then yields the solution $x=3$. Thus the solution to the above set of linear equations is $(x,y) = (3,-2)$.

MATRIX NOTATION This problem can be written in matrix notation as

More compactly, this problem can be written as $A v = r$ where

is the coefficient matrix, $v = (x, y)^T$ is the vector of unknowns, and $r = (-3, 10)^T$ is the vector of right--hand side values. The superscript $T$ denotes transpose. The transpose of a row vector is a column vector.

The problem of solving for $x$ and $y$ can now be expressed as the problem of inverting the matrix $A$. If $A^{-1}$ denotes the inverse of $A$, then the solution is $v = A^{-1} r$.

It is straightforward (try it!) to verify that the inverse of $A$ is

That is, using matrix multiplication, $A^{-1} A = I$ where $I$ is the identity matrix:

If we apply $A^{-1}$ to the equation $A v = r$, the left--hand side becomes $A^{-1}Av = Iv = v$. The right--hand side is $A^{-1} r$. Thus, we have $v = A^{-1} r$, which can be written explicitly as

Exercise: Find the solution, $(x,y)$ by carrying out the multiplication of $A^{-1}$ and $r$ by hand.

Linear Algebra in Python These calculations are quite easy to carry out in Python. The syntax for defining the matrix $A$ as a two-dimensional array and computing its inverse $A^{-1}$ is

from matplotlib.pylab import *

A = array([[1,3],[2,-2]])
Ainv = inv(A) 

We can now define the right--hand side vector $r$ and compute the answer $A^{-1}r$ as follows:

r = array([[-3],[10]])
v = Ainv.dot(r)

Note that this is not the same thing as v = Ainv * r, which would simply do an element-by-element multiplication. More details about using numpy arrays for linear algebra can be found at the linalg scipy tutorial.

Inverting a matrix numerically can lead to numerical errors and can also be a slow process. Numpy includes the following function for solving the linear system $Av= r$:

v = solve(A,r)

The algorithm used by solve can be faster and more accurate than explicit matrix inversion.

For a simple problem such as this one, you can type the commands into an interactive python session. For more complicated problems, you will want to type your code into a text file and run it as a python script.

Going back to our statics problem, in linear algebra notion the problem reduces to solving

Exercise: Using values of $m = 14$, $\ell = 1.2$, and $g = 9.8$ in SI units and $\theta = 35^\circ$, solve this system of equations to find the Force of the wall on the beam and the tension in the cord.

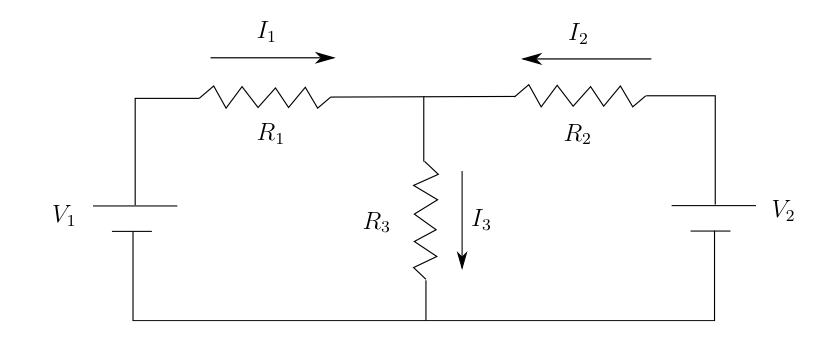
Assignment: Find the current $I_3$ in the circuit below by writing three Kirchoff's equations using matrix notation and the Python solve(A,r) function. Use the values $V_1 = 12, V_2 =9,R_1 =100,R_2 =120,R_3 =65$ in SI units.